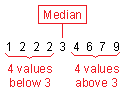
In a data set, there are the same number of values above the median as there are below. For instance, the median of the data set below is 3. Notice that there are 4 values below 3 and 4 values above 3.

It should be noted that if no entry in a data set is repeated, then the data set has no mode. Also, if two entries occur with the same greatest frequency, then each entry is a mode and the data set is called bimodal. (See also Section 9.3, Example 6.)

While the mean, median and mode each describe the "average" of a data set, there are advantages and disadvantages of using each. The mean takes into account every value, while the median and mode do not, perhaps making the mean more reliable. When there are outliers, however, the mean can be greatly affected while the median and mode will be unaffected. (You will learn more about outliers on pages 416 and 417.)

Keep in mind that you can use a spreadsheet to help determine the mean, median, and mode of a data set.

Age distribution charts can be constructed for many different reasons. Check out this chart, which shows the age distribution of the U.S. Congress.

Brazil's population pyramid is more bottom-heavy than the United States' pyramid. In Brazil, a relatively large percent of the population is between 0 and 15. Comparing the two pyramids, it appears that Brazil's mean, median, and mode ages are less than those of the United States.