Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

9.2 Describing "Average"

9.2 Describing "Average"
<
>
  • 1. Finding the Mean of the Heights of Basketball Players

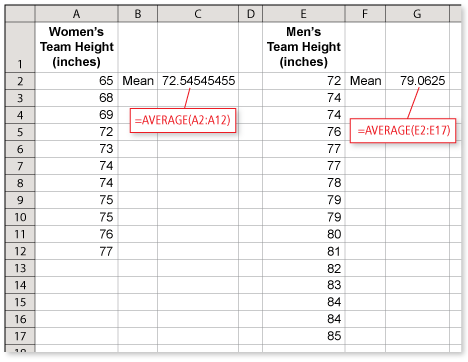
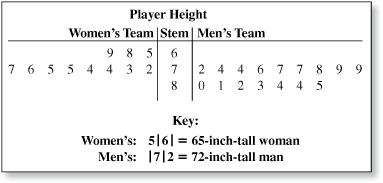
    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. Compare the mean of each data set. (See Example 1 and Example 2.)

    data folder

    • Worked-Out Solution

      Use the stem-and-leaf plot to write the heights (in inches) for each team in order.

      Women's team: 65, 68, 69, 72, 73, 74, 74, 75, 75, 76, 77

      Men's team: 72, 74, 74, 76, 77, 77, 78, 79, 79, 80, 81, 82, 83, 84, 84, 85

      To find the mean of each data set, add all the values and divide the result by the number of values.

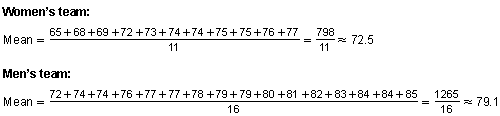
      The mean height for the women's team is about 72.5 inches and the mean height for the men's team is about 79.1 inches. So, the average player on the men's team is more than 6 inches taller than the average player on the women's team.

      Another way you can find the mean for each team is to use a spreadsheet.

       

      data folder

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   _     ______    _____     ______   _    _   
| || | ||  /_   _//  / ____||  /_   _// | \  / || 
| '--' ||   -| ||-  / //---`'   -| ||-  |  \/  || 
| .--. ||   _| ||_  \ \\___     _| ||_  | .  . || 
|_|| |_||  /_____//  \_____||  /_____// |_|\/|_|| 
`-`  `-`   `-----`    `----`   `-----`  `-`  `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 2. Finding the Mode of the Heights of Basketball Players

    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. What is the mode of each data set? (See Example 1 and Example 2.)

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

       _____   _    _     _____     ______   __   __  
  / ___// | || | ||  /  ___||  /_   _//  \ \\/ // 
  \___ \\ | || | || | // __     -| ||-    \   //  
  /    // | \\_/ || | \\_\ ||   _| ||_    / . \\  
 /____//   \____//   \____//   /_____//  /_//\_\\ 
`-----`     `---`     `---`    `-----`   `-`  --`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 3. Comparing the Median Heights of Two Basketball Teams

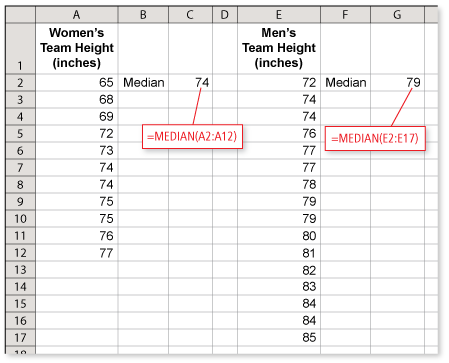
    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. Compare the median of each data set. (See Example 1 and Example 2.)

    data folder

    • Worked-Out Solution

      Use the stem-and-leaf plot to write the heights (in inches) for each team in order.

      Women's team: 65, 68, 69, 72, 73, 74, 74, 75, 75, 76, 77

      Men's team: 72, 74, 74, 76, 77, 77, 78, 79, 79, 80, 81, 82, 83, 84, 84, 85

      To find the median of each data set, find the middle number when there is an odd number of data, and find the mean of the middle two numbers when there is an even number of data.

      Women's team: There are 11 data, so the median is the middle value, 74.

      Men's team: There are 16 data, so the median is the mean of the middle two values, 79.

      The median height for the women's team is 74 inches. The median height for the men's team is 79 inches.

      Another way you can find the median for each team is to use a spreadsheet.

      data folder

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   _     _____     ______     ___              
| || | ||  |  ___||  /_   _//   / _ \\      ___   
| '--' ||  | ||__    `-| |,-   / //\ \\    /   || 
| .--. ||  | ||__      | ||   |  ___  ||  | [] || 
|_|| |_||  |_____||    |_||   |_||  |_||   \__ || 
`-`  `-`   `-----`     `-`'   `-`   `-`     -|_|| 
                                             `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 4. Finding the Percent of Basketball Players That Are at Least 7 Feet Tall

    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. What percent of the players on the men's team are at least 7 feet tall? (See Example 1 and Example 2.)

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ______     ___     _    _     ______    _____   
 /_   _//   / _ \\  | |  | ||  /_   _//  / ____|| 
 `-| |,-   | / \ || | |/\| ||   -| ||-  / //---`' 
   | ||    | \_/ || |  /\  ||   _| ||_  \ \\___   
   |_||     \___//  |_// \_||  /_____//  \_____|| 
   `-`'     `---`   `-`   `-`  `-----`    `----`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 5. Choosing the Best Measure of Central Tendency for Basketball Heights

    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. Which measure of central tendency best describes the average height of the women's basketball team? (See Example 1 and Example 2.)

    • Worked-Out Solution

      Ordered heights of the women's team: 65, 68, 69, 72, 73, 74, 74, 75, 75, 76, 77

      Mean =

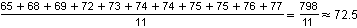
      Mode = 74, 75 (both heights occur twice in the data)

      Median = 74 (the middle value of the data)

      Sample answer:

      The mean height of 72.5 inches takes every entry into account, but is shorter than most of the heights because three of the women are quite a bit shorter than most of the others. The median height of 74 inches takes every entry into account and is within 2 inches of most of the heights. There are two modes. The mode of 74 inches is the same as the median, but the mode of 75 inches is greater than most of the data. It appears that the median of 74 inches best describes the average height of the players on the women's basketball team.

    Comments (1)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _____      ___      _____     ______    _  _   
 /  ___||   / _ \\   / ____||  /_   _//  | \| || 
| // __    | / \ || / //---`'   -| ||-   |  ' || 
| \\_\ ||  | \_/ || \ \\___     _| ||_   | .  || 
 \____//    \___//   \_____||  /_____//  |_|\_|| 
  `---`     `---`     `----`   `-----`   `-` -`
    Showing 1 comments
    Subscribe by RSS
    system user
    Guest   3 years ago |
    Math is cool
    1
  • 6. Choosing the Best Measure of Central Tendency for Basketball Heights

    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. Which measure of central tendency best describes the average height of the men's basketball team? (See Example 1 and Example 2.)

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _____     _____    __   _     ______    _____   
 |__  //   |  ___|| | || | ||  /_   _//  |__  //  
   / //    | ||__   | '--' ||   -| ||-     / //   
  / //__   | ||__   | .--. ||   _| ||_    / //__  
 /_____||  |_____|| |_|| |_||  /_____//  /_____|| 
 `-----`   `-----`  `-`  `-`   `-----`   `-----`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 7. Finding the Change in the Mean and Median Heights

    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. Suppose each height on the women's team is 2 inches greater. How does this affect the mean and the median of the data? (See Example 1 and Example 2.)

    • Worked-Out Solution

      Find the mean and median of the original heights.

      Ordered original heights:  65, 68, 69, 72, 73, 74, 74, 75, 75, 76, 77

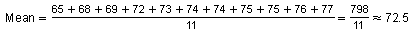
      Median = 74 (the middle value of the data)

      Find the mean and median of the increased heights.

      Ordered increased heights: 67, 70, 71, 74, 75, 76, 76, 77, 77, 78, 79

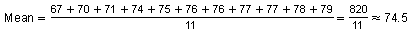
      Median = 76 (the middle value of the data)

      Find the change in the mean and median.

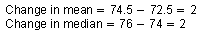
      If each height were 2 inches greater, then the mean and median would each be 2 inches greater.

      This is true for the mean because increasing each of the 11 heights by 2 inches increases the sum of the 11 heights by 11×2 inches, so the mean

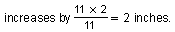
      This is true for the median because increasing each height by 2 inches increases the middle height by 2 inches.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _    __   __    _  __    _____    _    _   
| |  | ||  \ \\/ //  | |/ //  |  ___|| | |  | || 
| |/\| ||   \ ` //   | ' //   | ||__   | |/\| || 
|  /\  ||    | ||    | . \\   | ||__   |  /\  || 
|_// \_||    |_||    |_|\_\\  |_____|| |_// \_|| 
`-`   `-`    `-`'    `-` --`  `-----`  `-`   `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 8. Determining a Possible Starting Lineup

    The double stem-and-leaf plot shows the heights of a women's basketball team and a men's basketball team. The 5 starting players on the men's team have a mean height of 80.2 inches. Find the heights of 5 possible starters. (See Example 1 and Example 2.)

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _____     ______   __   _     ______    _____   
 /  ___||  /_   _// | || | ||  /_   _//  / ____|| 
| // __     -| ||-  | '--' ||   -| ||-  / //---`' 
| \\_\ ||   _| ||_  | .--. ||   _| ||_  \ \\___   
 \____//   /_____// |_|| |_||  /_____//  \_____|| 
  `---`    `-----`  `-`  `-`   `-----`    `----`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.