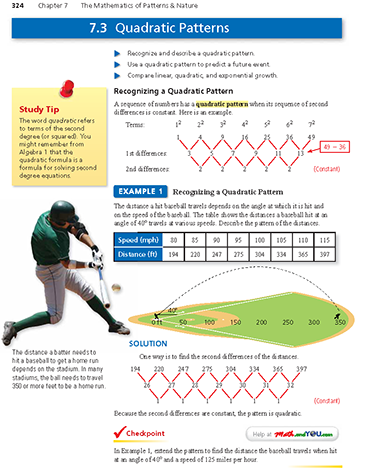
In Example 1, how do you know that the pattern is not linear? Because the first differences are not the same, the pattern cannot be linear. Also, notice that each difference is greater than the preceding difference, which means the rate of increase is increasing. This also supports the conclusion that the pattern is not linear. [Recall from Section 7.1 that a sequence of numbers has a linear pattern when each successive number increases (or decreases) by the same amount.]

In Example 1, note that the "speed" listed in the table is the velocity of the bat when it makes contact with the ball. Also, the situation in Example 1 has been simplified by not considering several factors, such as air resistance and air density.

Baseball has long been known as a national pastime. To buy tickets and get the latest news, scores, and videos of your favorite team, visit MLB.com.

Continue the pattern from when speed is 115 mph. The second difference is a constant 1, so the first difference between 115 mph and 120 mph increases to 33, and the first difference between 120 mph and 125 mph increases to 34, making the distance equal to 397 + 33 + 34 = 464 when speed is 125 mph.