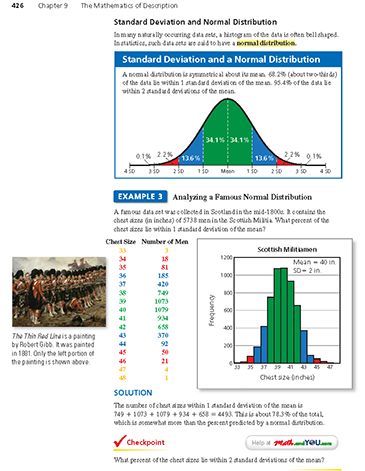
-
In the histogram in Example 3, "SD" stands for standard deviation. This notation will be used in graphs in the rest of this chapter.
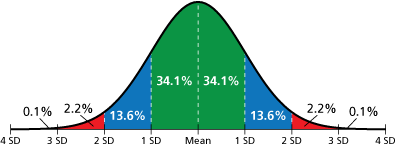
Here are some observations about normal distributions and the normal distribution graph on page 426 (also shown below).
- Because the graph is symmetrical about the mean, you can draw a vertical line through the mean and both halves are mirror images.
- 50% of the data lies below the mean and 50% of the data lies above the mean.
- The mean, median, and mode are equal.
- Data values that are farther than 2 standard deviations from the mean are considered unusual. Notice that 4.6% of the data values are farther than 2 standard deviations from the mean.
- Data values that are farther than 3 standard deviations from the mean are considered very unusual. Notice that 0.2% of the data values are farther than 3 standard deviations from the mean.
-
The National Council for Teachers of Mathematics provides a histogram tool that contains data sets of interesting examples. You can also enter your own data and create a histogram. To access the tool, visit NCTM Illuminations.
-
The number of chest sizes within 2 standard deviations of the mean is
185 + 420 + 749 + 1073 + 1079 + 934 + 658 + 370 + 92 = 5560.
This is
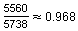 or about 96.8% of the total. This is close to the 95.4% predicted by a normal distribution.
or about 96.8% of the total. This is close to the 95.4% predicted by a normal distribution. -
Comments (0)
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use.Showing 0 commentsSubscribe by email Subscribe by RSSThere are no comments.