Math & YOU | 4.3 Exponential Decay

4.3 Exponential Decay

Page

Math Help

Here are some additional algebraic steps for finding the exponential decay rate in Example 5.

So, r = 0.05. Note that in the context of the problem in Example 5, r = 0.05 corresponds to an exponential decay rate of 5% every decade.

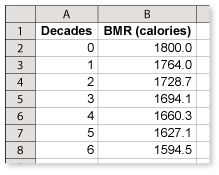
Download the spreadsheet to access the data used in Example 5.
Consumer Suggestion

To find out your basal metabolic rate (BMR), try this BMR calculator.
Checkpoint Solution

Begin by finding the rate of exponential decay.

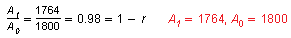
This implies r = 0.02 and that the man's BMR decays by 2% every decade.

By using the formula for exponential decay

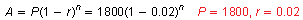
and a spreadsheet, you can see that the man's BMR drops to about 1660 calories after 4 decades.

So, he will be about 60 years old.
Comments (1)
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use.
Add new comment as Guest or Login. Not Registered? Register

Please enter the code displayed below:

______ _____ _ _ _ _ _ __ /_____// | ___|| | \ / || | || | || | |/ // `____ ` | ||__ | \/ || | || | || | ' // /___// | ||__ | . . || | \\_/ || | . \\ `__ ` |_____|| |_|\/|_|| \____// |_|\_\\ /_// `-----` `-` `-` `---` `-` --` `-`
Showing 1 comments

Sort by

Subscribe by email

Subscribe comments by email

Email

Subscribe by RSS

Guest 1 decade ago |

You should point out that the table on page 178 is only an estimate for a person's Basal Metabolic Rate. Some people keep a high BMR when they are older. Metabolic age is a number that comes from comparing your BMR with the BMR average of your chronological age group. A metabolic age number younger than your chronological age means that you are fitter than the average. An older metabolic age means that you are less fit than the average.

0 0