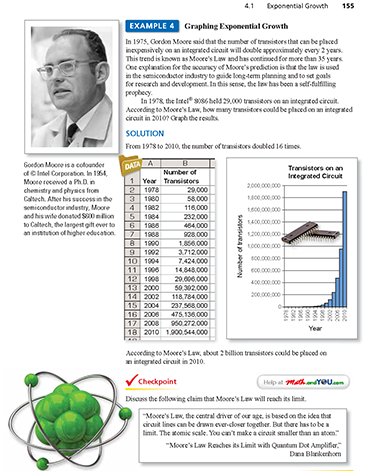
An integrated circuit is a microscopic array of electronic circuits and components that has been etched onto the surface of a semiconducting material such as silicon. It is called an integrated circuit because the components, circuits, and base material are all made from a single piece of silicon. An integrated circuit, more commonly known as a microchip, can be very complex, containing millions of elements. To learn more about the integrated circuit, read the article "The History of the Integrated Circuit" at Nobelprize.org. (Source: Encyclopedia.com)

In 1971, Intel began selling an integrated circuit that it described as the first "microprogrammable computer on a chip" with a price tag of $1,000. Intel and other manufacturers continued to refine the microchip, enabling the creation of personal computers.

Are you looking for a new computer? If so, visit this Computer Guide from Consumer Reports.

One integrated circuit has an area of about one square centimeter. It would take forty million atoms placed side by side to make a row about 1 centimeter in length. An integrated circuit that is one square centimeter could hold 40,000,000² = 1,600,000,000,000,000 or 1.6 quadrillion atoms.

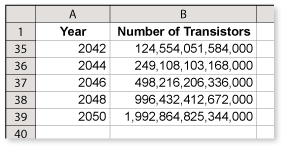
Suppose that a transistor became as small as a single atom. Moore's Law would be valid until at least 2050, as shown in the spreadsheet.

Advances in science, particularly the discovery of subatomic particles, could allow for even smaller transistors and integrated circuits in the future.