Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

9.4 Describing by Sampling

9.4 Describing by Sampling
<
>
  • 19. Mean Price of GPS Navigation Systems

    An electronics magazine reports that a 90% confidence interval for the mean price of GPS navigation systems is $178.75 to $211.87. Using the confidence interval, find the sample mean and the margin of error.

    • Worked-Out Solution

      The confidence interval is from $178.75 to $211.87. Recall that a confidence interval is given by

      Sample mean ± margin of error.

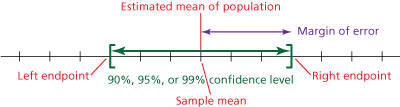
      The sample mean is the value in the middle of the confidence interval. To find the value that is in the middle of two numbers, add the numbers and divide by 2 as shown below.

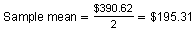
      To find the margin of error, subtract the sample mean from $211.87 because the distance from the sample mean to the right endpoint of the confidence interval is the margin of error.

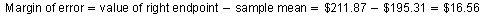
      So, the sample mean is $195.31 and the margin of error is $16.56.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

               __   __   _    _    __   __   _    _   
    ___    \ \\/ // | |  | ||  \ \\/ // | || | || 
   /   ||   \ ` //  | |/\| ||   \ ` //  | || | || 
  | [] ||    | ||   |  /\  ||    | ||   | \\_/ || 
   \__ ||    |_||   |_// \_||    |_||    \____//  
    -|_||    `-`'   `-`   `-`    `-`'     `---`   
     `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 20. Mean Salaries in Colorado

    A state agency reports that a 95% confidence interval for the mean annual salaries of employees in Colorado is $45,832 to $47,890. Using the confidence interval, find the sample mean and the margin of error.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _     _____     ______   __   __    _  __  
| \  / ||  |  ___||  /_____//  \ \\/ //  | |/ // 
|  \/  ||  | ||__    `____ `    \ ` //   | ' //  
| .  . ||  | ||__    /___//      | ||    | . \\  
|_|\/|_||  |_____||  `__ `       |_||    |_|\_\\ 
`-`  `-`   `-----`   /_//        `-`'    `-` --` 
                     `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 21. Mean Length of Stay in a Hospital

    A hospital reports that a 99% confidence interval for the mean length of stay (in days) of patients is 5.1 to 5.9. Using the confidence interval, find the sample mean and the margin of error.

    • Worked-Out Solution

      The confidence interval is from 5.1 days to 5.9 days. Recall that a confidence interval is given by

      Sample mean ± margin of error.

      The sample mean is the value in the middle of the confidence interval. To find the value that is in the middle of two numbers, add the numbers and divide by 2 as shown below.

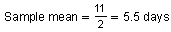
      To find the margin of error, subtract the sample mean from 5.9 days because the distance from the sample mean to the right endpoint of the confidence interval is the margin of error.

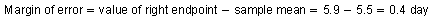
      So, the sample mean is 5.5 days and the margin of error is 0.4 day.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ______    ______   _    _     ______   _    _   
 /_   _//  /_   _// | \  / ||  /_   _// | || | || 
   | ||     -| ||-  |  \/  ||   -| ||-  | || | || 
  _| ||     _| ||_  | .  . ||   _| ||_  | \\_/ || 
 /__//     /_____// |_|\/|_||  /_____//  \____//  
 `--`      `-----`  `-`  `-`   `-----`    `---`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 22. Mean Weight of a Paint Can

    A company reports that a 95% confidence interval for the mean weight (in ounces) of filled paint cans is 159.97 to 160.03. Using the confidence interval, find the sample mean and the margin of error.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _    _    _                ___      _  __  
| \  / || | || | ||     ___     / _ \\   | |/ // 
|  \/  || | || | ||    /   ||  | / \ ||  | ' //  
| .  . || | \\_/ ||   | [] ||  | \_/ ||  | . \\  
|_|\/|_||  \____//     \__ ||   \___//   |_|\_\\ 
`-`  `-`    `---`       -|_||   `---`    `-` --` 
                         `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 23. Minimum Sample Size for the Mean Weight of Newborns

    For a 95% confidence level, the minimum sample size n needed to estimate the population mean is

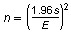
    where E is the margin of error and s is the population standard deviation. You want to estimate the mean weight of newborns within 0.25 pound of the population mean. Assume the population standard deviation is 1.3 pounds. Find the minimum sample size. If necessary, round your answer up to a whole number.

    • Worked-Out Solution

      You have the following information.

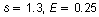
      Use the formula for minimum sample size.

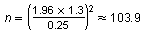
      Rounding up, the minimum sample size is 104 newborns.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ____     __   __              _____     ______  
 |  _ \\   \ \\/ //     ___    |  ___||  /_   _// 
 | |_| ||   \ ` //     /   ||  | ||__    `-| |,-  
 | .  //     | ||     | [] ||  | ||__      | ||   
 |_|\_\\     |_||      \__ ||  |_____||    |_||   
 `-` --`     `-`'       -|_||  `-----`     `-`'   
                         `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 24. Minimum Sample Size for the Number of Text Messages

    For a 95% confidence level, the minimum sample size n needed to estimate the population mean is

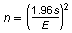
    where E is the margin of error and s is the population standard deviation. You want to estimate the mean number of text messages sent per day by 18- to 24-year-olds within 5 messages of the population mean. Assume the population standard deviation is 30 messages. Find the minimum sample size. If necessary, round your answer up to a whole number.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

                 ___      ____      _____     _  _   
  ____      / _ \\   |  _ \\   |  ___||  | \| || 
 |    \\   | / \ ||  | |_| ||  | ||__    |  ' || 
 | [] ||   | \_/ ||  | .  //   | ||__    | .  || 
 |  __//    \___//   |_|\_\\   |_____||  |_|\_|| 
 |_|`-`     `---`    `-` --`   `-----`   `-` -`  
 `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 25. Minimum Sample Size for the Mean Number of Hours of Television Watched

    For a 95% confidence level, the minimum sample size n needed to estimate the population mean is

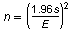
    where E is the margin of error and s is the population standard deviation. You want to estimate the mean number of hours of television watched per person per day within 0.1 hour of the population mean. Assume the population standard deviation is 1.5 hours. Find the minimum sample size. If necessary, round your answer up to a whole number.

    • Worked-Out Solution

      You have the following information.

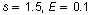
      Use the formula for minimum sample size.

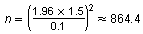
      Rounding up, the minimum sample size is 865 people.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

               _    _      _____     ___       _____  
  ____    | || | ||   / ___//   / _ \\    / ___// 
 |    \\  | || | ||   \___ \\  / //\ \\   \___ \\ 
 | [] ||  | \\_/ ||   /    // |  ___  ||  /    // 
 |  __//   \____//   /____//  |_||  |_|| /____//  
 |_|`-`     `---`   `-----`   `-`   `-` `-----`   
 `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 26. Minimum Sample Size for the Wait Time at the D.M.V.

    For a 95% confidence level, the minimum sample size n needed to estimate the population mean is

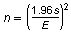
    where E is the margin of error and s is the population standard deviation. You want to estimate the mean number of minutes waiting at a department of motor vehicles office within 0.5 minute of the population mean. Assume the population standard deviation is 7 minutes. Find the minimum sample size. If necessary, round your answer up to a whole number.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _____     _    _     _  _      ___     _    _   
|  __ \\  | || | ||  | \| ||   / _ \\  | |  | || 
| |  \ || | || | ||  |  ' ||  | / \ || | |/\| || 
| |__/ || | \\_/ ||  | .  ||  | \_/ || |  /\  || 
|_____//   \____//   |_|\_||   \___//  |_// \_|| 
 -----`     `---`    `-` -`    `---`   `-`   `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.