Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

Chapter 8 Review Exercises

Chapter 8 Review Exercises
<
>
  • 7. Platonic Solids

    There are five Platonic solids: tetrahedron, cube, octahedron, dodecahedron, and icosahedron.

    Why do these solids make natural shapes for dice?

    • Worked-Out Solution

      Each of the Platonic solids is a natural shape for dice because, for each solid, the probability of landing on any one of the faces is the same.

      For instance, with a tetrahedron, each of the four faces has a one-fourth chance of landing down.

      With a cube, each of the six faces has a one-sixth chance of landing down (or landing up).

      In 1984, the author of this textbook patented a type of dice using dodecahedrons. The twelve faces have countable, recessed "dots" numbering one to six. Each total from one to six appears on precisely two opposite faces.

      To view the patent and a sketch of the dice, go to http://math.andyou.com/pdf/patent.pdf

      If you would like a pair of these dice, you can write to Jackie at feedback@AndYou.com. She will send you a pair free, while the supply lasts.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _  _    _    _    _____     _    _             
 | \| || | || | || |  __ \\  | || | ||   ____    
 |  ' || | || | || | |  \ || | || | ||  |    \\  
 | .  || | \\_/ || | |__/ || | \\_/ ||  | [] ||  
 |_|\_||  \____//  |_____//   \____//   |  __//  
 `-` -`    `---`    -----`     `---`    |_|`-`   
                                        `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 8. Platonic Solids

    There are five Platonic solids: tetrahedron, cube, octahedron, dodecahedron and icosahedron.

    Which shape is the best for dice? Why? Which is the worst? Why?

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

    __    __     ___      _____      ___     ______   
\ \\ / //   / _ \\   |__  //    / _ \\  |      \\ 
 \ \/ //   / //\ \\    / //    / //\ \\ |  --  // 
  \  //   |  ___  ||  / //__  |  ___  |||  --  \\ 
   \//    |_||  |_|| /_____|| |_||  |_|||______// 
    `     `-`   `-`  `-----`  `-`   `-` `------`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 9. Platonic Solids

    There are five Platonic solids: tetrahedron, cube, octahedron, dodecahedron, and icosahedron.

    A die has the shape of an icosahedron, with consecutively numbered sides starting at 1. What is the probability of rolling a number that is greater than 5?

    • Worked-Out Solution

      An icosahedron die has 20 sides, numbered

      1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20.

      When such a die is rolled, the probability of rolling a number greater than 5 is

    Comments (0)

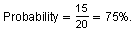
    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _     ______   _    _    _    _     ______  
| |  | ||  /_   _// | || | || | || | ||  /_   _// 
| |/\| ||   -| ||-  | || | || | || | ||    | ||   
|  /\  ||   _| ||_  | \\_/ || | \\_/ ||   _| ||   
|_// \_||  /_____//  \____//   \____//   /__//    
`-`   `-`  `-----`    `---`     `---`    `--`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 10. Platonic Solids

    There are only five Platonic solids. What is the definition of a Platonic solid?

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   __   _    _     _____     _____     ______  
 \ \\/ // | || | ||  /  ___||  |  ___||  /_   _// 
  \   //  | || | || | // __    | ||__      | ||   
  / . \\  | \\_/ || | \\_\ ||  | ||__     _| ||   
 /_//\_\\  \____//   \____//   |_____||  /__//    
 `-`  --`   `---`     `---`    `-----`   `--`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 11. Finding an Experimental Probability

    The tables show the results of a survey that asked adults whether they own an MP3 player.

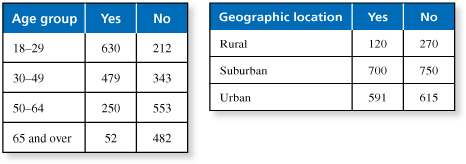
    Find the probability that an adult in each age group owns an MP3 player. Then describe the likelihood.

    • Worked-Out Solution

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

       _____    _____     _____     ______    ____    
  / ___//  |  ___||  |__  //   /_   _//  |  _ \\  
  \___ \\  | ||__      / //     -| ||-   | |_| || 
  /    //  | ||__     / //__    _| ||_   | .  //  
 /____//   |_____||  /_____||  /_____//  |_|\_\\  
`-----`    `-----`   `-----`   `-----`   `-` --`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 12. Finding an Experimental Probability

    The tables show the results of a survey that asked adults whether they own an MP3 player.

    Find the probability that an adult in each geographic location owns an MP3 player. Then describe the likelihood.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _  _    _    _     _  _     ______   _    _   
 | \| || | || | ||  | \| ||  /_   _// | \  / || 
 |  ' || | || | ||  |  ' ||   -| ||-  |  \/  || 
 | .  || | \\_/ ||  | .  ||   _| ||_  | .  . || 
 |_|\_||  \____//   |_|\_||  /_____// |_|\/|_|| 
 `-` -`    `---`    `-` -`   `-----`  `-`  `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.