To make a spreadsheet similar to the one in Example 3, use the steps below.

1. Enter the titles "Number," "Payoff," "Probability," and "Expected Value" into row 1.
2. Enter 1 into cell A2.
3. Enter the formula = A2 + 1 into cell A3.
4. Select cell A3. From the Edit menu, choose Copy.
5. Select cells A4 through A7. From the Edit menu, choose Paste.
6. Enter the title "Total" into cell A8.
7. Enter the formula = 3*A2 into cell B2.
8. Select cell B2. From the Edit menu, choose Copy.
9. Select cells B3 through B7. From the Edit menu, choose Paste.
10. Enter 0.1667 into cell C2.
11. Select cell C2. From the Edit menu, choose Copy.
12. Select cells C3 through C7. From the Edit menu, choose Paste.
13. Enter the formula = B2*C2 into cell D2.
14. Select cell D2. From the Edit menu, choose Copy.
15. Select cells D3 through D7. From the Edit menu, choose Paste.
16. Enter the formula =SUM(D2:D7) into cell D8.

To format the cells, use the steps below.

1. Select cells B2 through B7.
2. From the Format menu, choose Cells....
3. In the Format Cells dialog, select the Number tab.
4. From the Category: list, select Currency.
5. For Decimal places:, enter 2. For Symbol, choose $ from the drop down list. Then click OK.
6. Repeat Steps 1-5 for cells D2 through D8.
7. Select cells C2 through C7.
8. From the Format menu, choose Cells....
9. In the Format Cells dialog, select the Number tab.
10. From the Category: list, select Percentage.
11. For Decimal places:, enter 2. Then click OK.

A coin toss is used at the beginning of a football game. You may have used a coin toss or two to settle an argument. For a few tips to help you win a coin toss, visit Wired.

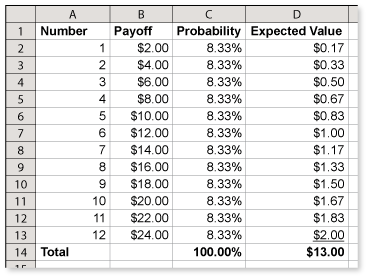
A spreadsheet showing the number of dots, payoff, probability, and expected value for each possible roll of the die is shown below.

The probability of rolling each number of dots is 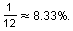The expected value for each number of dots is the payoff multiplied by the probability of that roll happening. The expected value of the offer is the sum of the individual expected values. I would take the uncle's offer. It has the highest expected value, $13, compared to $10 and $10.50, and the highest potential payout, $24, compared to $20 and $18.