Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

8.2 Estimating Likelihood

8.2 Estimating Likelihood
<
>
  • Math Help

    The graph shows the number of combinations assigned to each of the 14 teams in the NBA Draft Lottery. In Example 2, you determined the probability that the team with the worst record wins the first pick is 25%. The graph supports this conclusion because the height of the bar for the team with the worst record is greater than the heights of all the other bars.

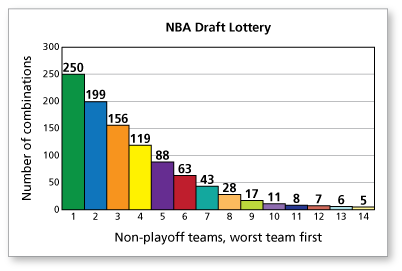
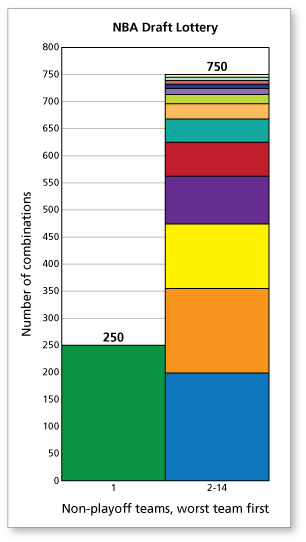
    Is it more likely that the team with the worst record will not win the first pick? Using the graph, imagine stacking all of the bars for the other 13 teams, as shown in the figure below. The height of this stack is greater than the height of the bar for the worst team. So, it is more likely that the team with the worst record will not win the first pick.

  • Consumer Suggestion

    If you're a fan of the NBA you might want to check out the Sports Authority, where you can get accessories and apparel for all your favorite teams.

  • Checkpoint Solution
    1. A spreadsheet showing the probability for each team is shown below.

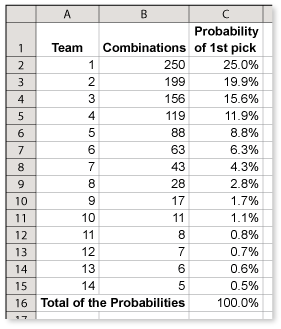
    2. The total of the probabilities column is 100%. The sum of the probabilities of any comprehensive list of events will be 100%.
  • Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ____       ___      ____     _    _    __   __  
 |  _ \\    / _ \\   |  _ \\  | || | ||  \ \\/ // 
 | |_| ||  / //\ \\  | |_| || | || | ||   \   //  
 | .  //  |  ___  || | .  //  | \\_/ ||   / . \\  
 |_|\_\\  |_||  |_|| |_|\_\\   \____//   /_//\_\\ 
 `-` --`  `-`   `-`  `-` --`    `---`    `-`  --`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.