Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

7.4 Fibonacci & Other Patterns

7.4 Fibonacci & Other Patterns
<
>
  • 21. Golden Angle

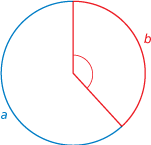
    In the figure, the golden angle is the angle subtended by the smaller red arc.

    Using the Internet, what is the measure of the golden angle in degrees? Explain why this angle is called the golden angle.

    • Worked-Out Solution

      The golden angle is formed by dividing the circumference of a circle into two parts so that the ratio of the larger part (blue arc) to the smaller part (red arc) is the golden ratio.

      The measure (using the Internet) of the golden angle is about 137.51°.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

       _____   __   __    _____     ______    _____   
  / ___//  \ \\/ //  / ____||  /_   _//  /  ___|| 
  \___ \\   \ ` //  / //---`'   -| ||-  | // __   
  /    //    | ||   \ \\___     _| ||_  | \\_\ || 
 /____//     |_||    \_____||  /_____//  \____//  
`-----`      `-`'     `----`   `-----`    `---`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 22. Golden Angle

    In the figure, the golden angle is the angle subtended by the smaller red arc. Using the Internet, describe how the golden angle is related to phyllotaxis.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _    __   __  __    __     ___     ______   
| || | ||  \ \\/ // \ \\ / //   / _ \\  |      \\ 
| || | ||   \ ` //   \ \/ //   / //\ \\ |  --  // 
| \\_/ ||    | ||     \  //   |  ___  |||  --  \\ 
 \____//     |_||      \//    |_||  |_|||______// 
  `---`      `-`'       `     `-`   `-` `------`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 23. Golden Triangle

    A golden triangle is an isosceles triangle in which the ratio of the length of one of the longer sides to the length of the shorter side is the golden ratio. The base angles are 72° each, and the smaller angle is 36°.

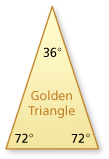
    Does a triangle with the following side lengths approximate a golden triangle? Explain.

    1. 8 ft, 8 ft, 5 ft
    2. 21 cm, 13 cm, 18 cm
    3. 55 m, 34 m, 55 m
    4. 10 in., 14 in., 14 in.
    • Worked-Out Solution
      1. Yes, because the ratio of 8 to 5 is 1.6. This is close to the golden ratio.
      2. No, because this is not an isosceles triangle.
      3. Yes, because the ratio of 55 to 34 is about 1.62. This is very close to the golden ratio.
      4. No, because the ratio of 14 to 10 is 1.4. This is not very close to the golden ratio.
    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     ______      ___                 ___      _____   
|      \\   / _ \\      ___     / _ \\   /  ___|| 
|  --  //  / //\ \\    /   ||  | / \ || | // __   
|  --  \\ |  ___  ||  | [] ||  | \_/ || | \\_\ || 
|______// |_||  |_||   \__ ||   \___//   \____//  
`------`  `-`   `-`     -|_||   `---`     `---`   
                         `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 24. Golden Triangle

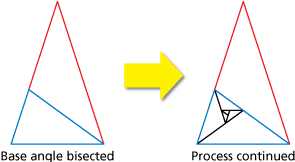
    A golden triangle is an isosceles triangle in which the ratio of the length of one of the longer sides to the length of the shorter side is the golden ratio. The base angles are 72° each, and the smaller angle is 36°.

    When a base angle of a golden triangle is bisected, the angle bisector divides the opposite side in a golden ratio and forms two smaller isosceles triangles. The blue triangle (shown below) that is created from the bisection is a golden triangle. This process can be continued indefinitely, creating smaller and smaller golden triangles. Use the bisection process of a golden triangle, a compass, and a ruler to draw the Fibonacci spiral.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

    __    __   _    _                ___              
\ \\ / // | || | ||   ____      / _ \\    ____    
 \ \/ //  | || | ||  |    \\   / //\ \\  |    \\  
  \  //   | \\_/ ||  | [] ||  |  ___  || | [] ||  
   \//     \____//   |  __//  |_||  |_|| |  __//  
    `       `---`    |_|`-`   `-`   `-`  |_|`-`   
                     `-`                 `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 25. Pentagon

    The figure is a pentagon with all its diagonals drawn. How are the diagonals and the sides related to the golden ratio?

    • Worked-Out Solution

      The ratio of any diagonal to any side is equal to the golden ratio.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ______   __   __    _  __    ______   __   _   
 /_____//  \ \\/ //  | |/ //  /_   _// | || | || 
 `____ `    \ ` //   | ' //    -| ||-  | '--' || 
 /___//      | ||    | . \\    _| ||_  | .--. || 
 `__ `       |_||    |_|\_\\  /_____// |_|| |_|| 
 /_//        `-`'    `-` --`  `-----`  `-`  `-`  
 `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 26. Golden Triangle

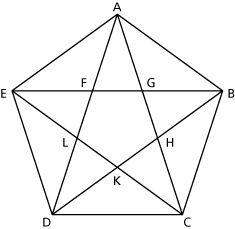
    A golden triangle is an isosceles triangle in which the ratio of the length of one of the longer sides to the length of the shorter side is the golden ratio. The base angles are 72° each, and the smaller angle is 36°.

    How many golden triangles can you find in the figure?

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ______     ___     _    _     _____   __    __  
 /_   _//   / _ \\  | \  / ||  |  ___|| \ \\ / // 
 `-| |,-   | / \ || |  \/  ||  | ||__    \ \/ //  
   | ||    | \_/ || | .  . ||  | ||__     \  //   
   |_||     \___//  |_|\/|_||  |_____||    \//    
   `-`'     `---`   `-`  `-`   `-----`      `
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.