-
The sequence of triangular numbers is
1, 3, 6, 10, 15, 21, 28, 36, 45, ....
-
The nth triangular number is the sum of the first n whole numbers.
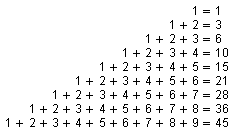
Comments (0)These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use.Showing 0 commentsSubscribe by email Subscribe by RSSThere are no comments. -
-
The sequence of triangular numbers is
1, 3, 6, 10, 15, 21, 28, 36, 45, ....
Describe how the sequence of triangular numbers is related to the following diagram. (See Example 5 and Example 6.)
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use. -
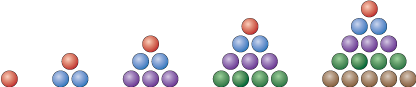
The sequence of triangular numbers is
1, 3, 6, 10, 15, 21, 28, 36, 45, ....
Is 115 a triangular number? Explain your reasoning. (See Example 5 and Example 6.)
-
The nth triangular number is the sum of the first n whole numbers.

By continuing the pattern, you can see that 115 is not a triangular number.
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use. -
-
The Lucas sequence is named in honor of mathematician François Édouard Anatole Lucas.
The Lucas sequence is
1, 3, 4, 7, 11, 18, 29, 47, 76,....
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use. -
The Lucas sequence is named in honor of mathematician François Édouard Anatole Lucas.
The Lucas sequence is
1, 3, 4, 7, 11, 18, 29, 47, 76, ....
Describe how the Lucas sequence is related to the cactus. (See Example 5 and Example 6.)

-
When looking down on the cactus, there are two sets of spirals. One is clockwise and the other is counterclockwise. The one set has 18 spirals and the other set has 11 spirals.
The numbers 11 and 18 are the 5th and 6th numbers of the Lucas sequence.
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use. -
-
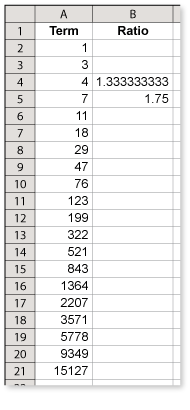
Use the spreadsheet to find the ratio of successive Lucas numbers. What number do you approach as the numbers get larger? (See Example 5 and Example 6.)
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use.