Math & YOU | 7.4 Fibonacci & Other Patterns

7.4 Fibonacci & Other Patterns

Page

Math Help

Although the Fibonacci sequence starts with 0 and 1, a general Fibonacci sequence can start with other numbers. For instance, in Example 1, the number of breeding pairs for each month starts with 1 and 1. So, the number of pairs follows the Fibonacci pattern

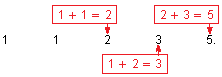
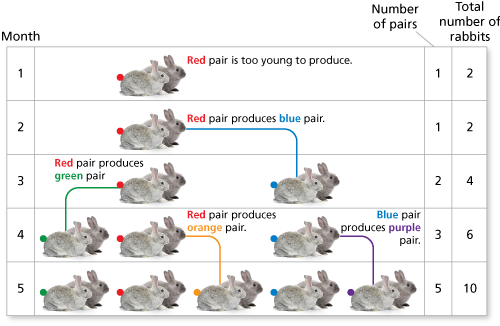
In the solution to Example 1, note that the table lists the number of breeding pairs for each month. To determine the total number of rabbits for each month, multiply the number of pairs by 2. The total number of rabbits is shown in the 4th column of the table below.
Consumer Suggestion

Rabbits can make great pets, but you may want to read this Humane Society article or watch this video before you decide to get one. If you decide you want a rabbit, read these tips on welcoming your new pet rabbit home.
Checkpoint Solution

Begin by entering the data into a spreadsheet. Then create a scatter plot showing the two growth patterns.

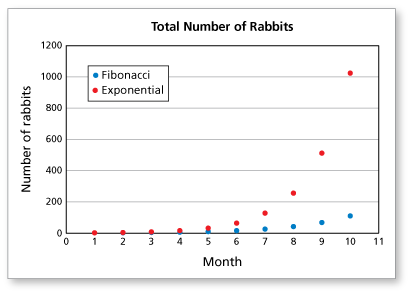
The number of rabbits with the exponential pattern is greater than or equal to that of the Fibonacci pattern at every point. With the exponential pattern, the number doubles each month while the Fibonacci sequence of rabbits increases at a slower rate.
Comments (2)
These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
When posting a comment, you agree to our Terms of Use.
Add new comment as Guest or Login. Not Registered? Register

Please enter the code displayed below:

______ _ _ __ __ _____ ___ /_ _// | \| || \ \\/ // | __ \\ / || -| ||- | ' || \ ` // | | \ || | [] || _| ||_ | . || | || | |__/ || \__ || /_____// |_|\_|| |_|| |_____// -|_|| `-----` `-` -` `-`' -----` `-`
Showing 2 comments

Sort by

Subscribe by email

Subscribe comments by email

Email

Subscribe by RSS

Cody (moderator)1 decade ago |

While Fibonacci numbers commonly occur in nature, they are used on occasion as a design element in man-made structures. To see an example of a building that uses the Fibonacci numbers as a design element click here.

http://www.andyou.com/blog/math-in-the-news/math-in-the-news-fibonacci-sequence/

1 0

Ron Larson (author)1 decade ago |

Fibonacci numbers have interested people for many years. You can read more about this interest by looking up the Fibonacci Association on a search engine.

1 0