Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

7.3 Quadratic Patterns

7.3 Quadratic Patterns
<
>
  • 7. Stopping a Car

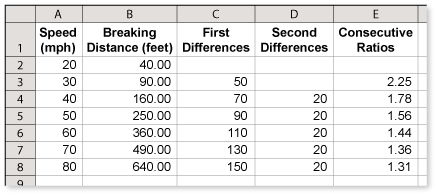
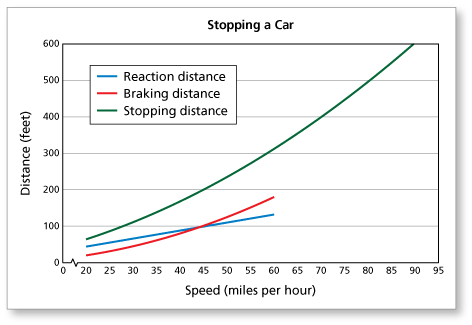
    Assuming proper operation of the brakes on a vehicle, the minimum stopping distance is the sum of the reaction distance and the braking distance. The reaction distance is the distance the car travels before the brakes are applied. The braking distance is the distance a car travels after the brakes are applied but before the car stops. A reaction time of 1.5 seconds is used in the graph.

    Does the graph of the stopping distance appear to be linear or quadratic? Explain your reasoning. (See Example 3.)

    • Worked-Out Solution

      The graph of the stopping distance appears to be quadratic. The stopping distance is clearly not linear, because the green graph is not a line.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   __     ___      _____      ___     _    _   
 \ \\/ //   / _ \\   |__  //    / _ \\  | |  | || 
  \   //   | / \ ||    / //    / //\ \\ | |/\| || 
  / . \\   | \_/ ||   / //__  |  ___  |||  /\  || 
 /_//\_\\   \___//   /_____|| |_||  |_|||_// \_|| 
 `-`  --`   `---`    `-----`  `-`   `-` `-`   `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 8. Stopping a Car

    Assuming proper operation of the brakes on a vehicle, the minimum stopping distance is the sum of the reaction distance and the braking distance. The reaction distance is the distance the car travels before the brakes are applied. The braking distance is the distance a car travels after the brakes are applied but before the care stops. A reaction time of 1.5 seconds is used in the graph.

    Does the graph of the reaction distance appear to be linear or quadratic? Explain your reasoning. (See Example 3.)

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _____     ______   __   _    __   __    _  __  
 / ____||  /_   _// | || | ||  \ \\/ //  | |/ // 
/ //---`'   -| ||-  | '--' ||   \ ` //   | ' //  
\ \\___     _| ||_  | .--. ||    | ||    | . \\  
 \_____||  /_____// |_|| |_||    |_||    |_|\_\\ 
  `----`   `-----`  `-`  `-`     `-`'    `-` --`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 9. Stopping Distance

    Assuming proper operation of the brakes on a vehicle, the minimum stopping distance is the sum of the reaction distance and the braking distance.The reaction distance is the distance the car travels before the brakes are applied. The braking distance is the distance a car travels after the brakes are applied but before the car stops. A reaction time of 1.5 seconds is used in the graph.

    Use the graph to predict the stopping distance at 90 miles per hour. (See Example 3.)

    • Worked-Out Solution

      To predict the stopping distance at 90 miles per hour, extend the graph. The stopping distance is about 600 feet.

    Comments (1)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   __     ___      ______    ______   _    _   
 \ \\/ //   / _ \\   /_   _//  /_   _// | \  / || 
  \   //   / //\ \\  `-| |,-    -| ||-  |  \/  || 
  / . \\  |  ___  ||   | ||     _| ||_  | .  . || 
 /_//\_\\ |_||  |_||   |_||    /_____// |_|\/|_|| 
 `-`  --` `-`   `-`    `-`'    `-----`  `-`  `-`
    Showing 1 comments
    Subscribe by RSS
    system user
    Guest   5 years ago |
    Guest
    0
  • 10. Braking Distance

    Assuming proper operation of the brakes on a vehicle, the minimum stopping distance is the sum of the reaction distance and the braking distance. The reaction distance is the distance the car travels before the brakes are applied. The braking distance is the distance a car travels after the brakes are applied but before the car stops. A reaction time of 1.5 seconds is used in the graph.

    The braking distance at 35 miles per hour is about 60 feet. Does this mean that the braking distance at 70 miles per hour is about 120 feet? Explain. (See Example 3.)

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _  __   __   __    _____     ______    _____   
 | |/ //  \ \\/ //  / ____||  /_   _//  |__  //  
 | ' //    \ ` //  / //---`'   -| ||-     / //   
 | . \\     | ||   \ \\___     _| ||_    / //__  
 |_|\_\\    |_||    \_____||  /_____//  /_____|| 
 `-` --`    `-`'     `----`   `-----`   `-----`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 11. Slippery Road

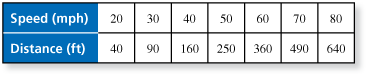
    The braking distance of a car depends on the friction between the tires and the road. The table shows the braking distance for a car on a slippery road at various speeds. Is the pattern quadratic? Explain. (See Example 4.)

    data folder

    • Worked-Out Solution

      To decide whether the data follows a quadratic pattern, enter it into a spreadsheet and compare the second differences. They are all equal. So, the pattern is quadratic.

      data folder

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _  __    ______    _  _    _    _     ______  
 | |/ //  /_   _//  | \| || | || | ||  /_   _// 
 | ' //    -| ||-   |  ' || | || | ||    | ||   
 | . \\    _| ||_   | .  || | \\_/ ||   _| ||   
 |_|\_\\  /_____//  |_|\_||  \____//   /__//    
 `-` --`  `-----`   `-` -`    `---`    `--`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 12. Braking Distance on a Slippery Road

    The braking distance of a car depends on the friction between the tires and the road. The table shows the braking distance for a car on a slippery road at various speeds. Graph the data in the table. Compare this graph to the graph from Exercises 7-10. (See Example 4.)

    data folder

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _      ___      ______   __   __            
| || | ||   / _ \\   /_   _//  \ \\/ //     ___   
| || | ||  / //\ \\    | ||     \ ` //     /   || 
| \\_/ || |  ___  ||  _| ||      | ||     | [] || 
 \____//  |_||  |_|| /__//       |_||      \__ || 
  `---`   `-`   `-`  `--`        `-`'       -|_|| 
                                             `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.