Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

7.2 Exponential Patterns

7.2 Exponential Patterns
<
>
  • 21. Logistic Growth Rate

    The formula for the logistic growth rate is

    where r0 is the intrinsic growth rate in decimal form.

    The population of squirrels in a forest is growing logistically. The intrinsic growth rate is 40% per year, and the maximum sustainable population is 5000. Find the rate at which the population is growing when the population reaches each size.

    1. 100
    1. 2000
    1. 4500
    • Worked-Out Solution

      1. When the population is 100 squirrels, the rate at which the population is growing is

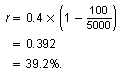
      2. When the population is 2000 squirrels, the rate at which the population is growing is

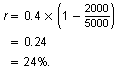
      3. When the population is 4500 squirrels, the rate at which the population is growing is

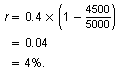
    Comments (2)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   _     _____              _    _   __    __  
| || | ||  |  ___||   ____    | || | || \ \\ / // 
| '--' ||  | ||__    |    \\  | || | ||  \ \/ //  
| .--. ||  | ||__    | [] ||  | \\_/ ||   \  //   
|_|| |_||  |_____||  |  __//   \____//     \//    
`-`  `-`   `-----`   |_|`-`     `---`       `     
                     `-`
    Showing 2 comments
    Subscribe by RSS
    system user
    Cody (moderator)1 decade ago |
    Thank you for letting me know. I will make sure that the formula is corrected.
    0
    system user
    Guest   1 decade ago |
    The formula given on page 321in the book is incorrect. The "1" should be inside the parenthesis.
    0
  • 22. Logistic Growth Rate

    The formula for the logistic growth rate is

    where r0 is the intrinsic growth rate in decimal form.

    The population of raccoons in a forest is growing logistically. The intrinsic growth rate is 50% per year, and the maximum sustainable population is 2000. Find the rate at which the population is growing when the population reaches each size.

    1. 200
    2. 1000
    3. 1800
    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   __    ______   _____       ___      _  __  
 \ \\/ //  /_   _// |  __ \\    / _ \\   | |/ // 
  \   //    -| ||-  | |  \ ||  | / \ ||  | ' //  
  / . \\    _| ||_  | |__/ ||  | \_/ ||  | . \\  
 /_//\_\\  /_____// |_____//    \___//   |_|\_\\ 
 `-`  --`  `-----`   -----`     `---`    `-` --`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 23. Maximum Sustainable Population

    The formula for the logistic growth rate is

    where r0 is the intrinsic growth rate in decimal form.

    What is the growth rate when a population is at the maximum sustainable population? Explain.

    • Worked-Out Solution

      When a population reaches its maximum sustainable population, the growth rate is

      This makes sense because if a population is at its maximum, it can't grow any larger.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

                _____     _____     _____             
  ____     |  ___||  |__  //   |  ___||     ___   
 |    \\   | ||__      / //    | ||__      /   || 
 | [] ||   | ||__     / //__   | ||__     | [] || 
 |  __//   |_____||  /_____||  |_____||    \__ || 
 |_|`-`    `-----`   `-----`   `-----`      -|_|| 
 `-`                                         `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 24. Maximum Sustainable Population

    The formula for the logistic growth rate is

    where r0 is the intrinsic growth rate in decimal form.

    Describe the growth rate when a population exceeds the maximum sustainable population. Explain what this represents in nature.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     __   __   __   __               ___              
 \ \\/ //  \ \\/ //     ___     / _ \\      ___   
  \   //    \ ` //     /   ||  / //\ \\    /   || 
  / . \\     | ||     | [] || |  ___  ||  | [] || 
 /_//\_\\    |_||      \__ || |_||  |_||   \__ || 
 `-`  --`    `-`'       -|_|| `-`   `-`     -|_|| 
                         `-`                 `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 25. Superexponential Growth

    A population undergoes superexponential growth when the growth rate increases exponentially over time.

    A population of 100 locusts is introduced to a new area. The initial growth rate is 50% per year. Make a table comparing the population of the locusts over a 10-year period when the growth rate remains constant (exponential) and when the growth rate increases by 20% each year (superexponential). Then make a scatter plot comparing the two data sets.

    data folder

    • Worked-Out Solution

      The two population growth patterns are shown in the spreadsheet.

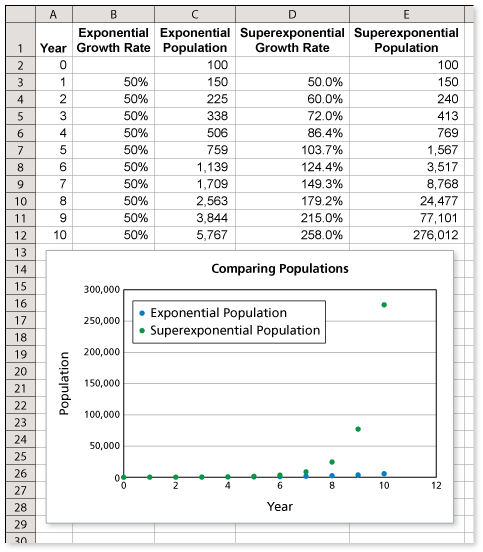
      Notice that there is no comparison in the two populations. With exponential growth, the population is about 6000 locusts after 10 years. But, with superexponential growth, the population exceeds 270,000 million after 10 years.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ____     _    _    __   __     ___      _____   
 |  _ \\  | || | ||  \ \\/ //   / _ \\   |__  //  
 | |_| || | || | ||   \   //   | / \ ||    / //   
 | .  //  | \\_/ ||   / . \\   | \_/ ||   / //__  
 |_|\_\\   \____//   /_//\_\\   \___//   /_____|| 
 `-` --`    `---`    `-`  --`   `---`    `-----`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 26. Superexponential Growth

    A population undergoes superexponential growth when the growth rate increases exponentially over time.

    A population of 50 frogs is introduced to a new area. The initial growth rate is 60% per year. Make a table comparing the population of the frogs over a 10-year period when the growth rate remains constant (exponential) and when the growth rate increases by 10% each year (superexponential). Then make a scatter plot comparing the two data sets.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _      ___      ______     ___              
| |  | ||   / _ \\   /_   _//   / _ \\      ___   
| |/\| ||  | / \ ||    | ||    / //\ \\    /   || 
|  /\  ||  | \_/ ||   _| ||   |  ___  ||  | [] || 
|_// \_||   \___//   /__//    |_||  |_||   \__ || 
`-`   `-`   `---`    `--`     `-`   `-`     -|_|| 
                                             `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 27. Riddle of the Lily Pad

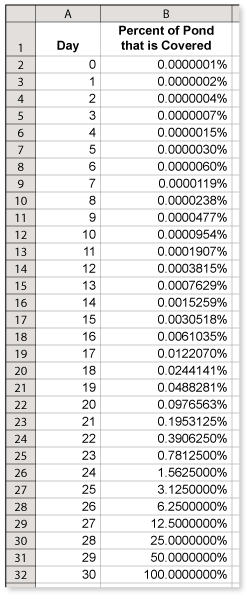
    A single lily pad lies on the surface of a pond. Each day the number of lily pads doubles until the entire pond is covered on day 30. On what day is the pond half-covered?

    data folder

    • Worked-Out Solution

      Because the number of lily pads is doubling every day, the pond is half covered on day 29. The spreadsheet shows the percent of the pond that is covered each day.

      data folder

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _____    __   __    _____    __   __    _____   
 |__  //   \ \\/ //  / ____||  \ \\/ //  |__  //  
   / //     \ ` //  / //---`'   \ ` //     / //   
  / //__     | ||   \ \\___      | ||     / //__  
 /_____||    |_||    \_____||    |_||    /_____|| 
 `-----`     `-`'     `----`     `-`'    `-----`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 28. Mutant Plant

    A mutant strain of water plant covers 100 square feet of the surface of a lake. The lake has a surface area of about 1,000,000 square feet. The surface area covered by the plant increases by 200% each day. You can clear 5000 square feet of plant cover in 1 day. During what day do you have to begin clearing the plant cover to stop the plant from spreading across the entire lake?

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

     _    _      ___     _    _     _____     ______  
| \  / ||   / _ \\  | |  | ||  |  ___||  /_   _// 
|  \/  ||  / //\ \\ | |/\| ||  | ||__      | ||   
| .  . || |  ___  |||  /\  ||  | ||__     _| ||   
|_|\/|_|| |_||  |_|||_// \_||  |_____||  /__//    
`-`  `-`  `-`   `-` `-`   `-`  `-----`   `--`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.