Ron Larson
Browse the Topics, Table of Contents, and Index
Follow us:
Twitter Facebook

4.3 Exponential Decay

4.3 Exponential Decay
<
>
  • 19. Social Media

    A video posted on a social media website has 1024 views on day 1. The number of views increases by 50% each day through day 10, and then decreases by 10% each day through day 30. Write a formula that represents the number of daily views for the first 10 days.

    • Worked-Out Solution

      Use the formula for exponential growth.

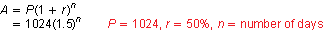
    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

                ______    _____    __   __   ______   
  ____     /_   _//  /  ___||  \ \\/ // |      \\ 
 |    \\    -| ||-  | // __     \ ` //  |  --  // 
 | [] ||    _| ||_  | \\_\ ||    | ||   |  --  \\ 
 |  __//   /_____//  \____//     |_||   |______// 
 |_|`-`    `-----`    `---`      `-`'   `------`  
 `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 20. Social Media

    A video posted on a social media website has 1024 views on day 1. The number of views increases by 50% each day through day 10, and then decreases by 10% each day through day 30. How many views does the video have on day 10?

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

                _____                ___      ______  
    ___    |  ___||     ___     / _ \\   /_   _// 
   /   ||  | ||__      /   ||  | / \ ||    | ||   
  | [] ||  | ||__     | [] ||  | \_/ ||   _| ||   
   \__ ||  |_____||    \__ ||   \___//   /__//    
    -|_||  `-----`      -|_||   `---`    `--`     
     `-`                 `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 21. Social Media

    A video posted on a social media website has 1024 views on day 1. The number of views increases by 50% each day through day 10, and then decreases by 10% each day through day 30. Write a formula that represents the number of daily views for day 10 through day 30.

    • Worked-Out Solution

      Use the formula for exponential decay.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      ______   __   __   _    _    _    _     ______  
 /_   _//  \ \\/ // | \  / || | || | ||  /_   _// 
   | ||     \ ` //  |  \/  || | || | ||  `-| |,-  
  _| ||      | ||   | .  . || | \\_/ ||    | ||   
 /__//       |_||   |_|\/|_||  \____//     |_||   
 `--`        `-`'   `-`  `-`    `---`      `-`'
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 22. Social Media

    A video posted on a social media website has 1024 views on day 1. The number of views increases by 50% each day through day 10, and then decreases by 10% each day through day 30. Sketch a graph showing the number of daily views for the 30 days.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

      _____      ___      ____     _    _    _    _   
 /  ___||   / _ \\   |  _ \\  | || | || | \  / || 
| // __    | / \ ||  | |_| || | || | || |  \/  || 
| \\_\ ||  | \_/ ||  | .  //  | \\_/ || | .  . || 
 \____//    \___//   |_|\_\\   \____//  |_|\/|_|| 
  `---`     `---`    `-` --`    `---`   `-`  `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 23. Social Media

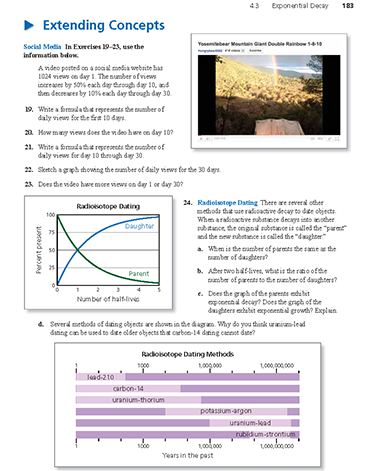
    A video posted on a social media website has 1024 views on day 1. The number of views increases by 50% each day through day 10, and then decreases by 10% each day through day 30. Does the video have more views on day 1 or day 30?

    • Worked-Out Solution

      Use the formula for exponential decay.

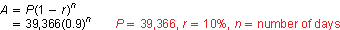
      Notice that the 10th day is represented by n = 0.

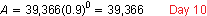
      By this reasoning, the 30th day is represented by n = 20.

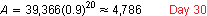
      So, with a 10% decrease each day for days 11 through 30, you would expect the number of views to have dropped to around 4800. The video had only 1024 views on day 1. So, it had more views on day 30.

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

       _____    _____    _    _    __   __    _____   
  / ___//  |  ___|| | |  | ||  \ \\/ //  |__  //  
  \___ \\  | ||__   | |/\| ||   \ ` //     / //   
  /    //  | ||__   |  /\  ||    | ||     / //__  
 /____//   |_____|| |_// \_||    |_||    /_____|| 
`-----`    `-----`  `-`   `-`    `-`'    `-----`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
  • 24. Radioisotope Dating

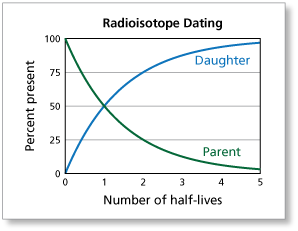
    There are several other methods that use radioactive decay to date objects. When a radioactive substance decays into another substance, the original substance is called the "parent" and the new substance is called the "daughter."

    a. When is the number of parents the same as the number of daughters?

    b. After two half-lives, what is the ratio of the number of parents to the number of daughters?

    c. Does the graph of the parents exhibit exponential decay? Does the graph of the daughters exhibit exponential growth? Explain.

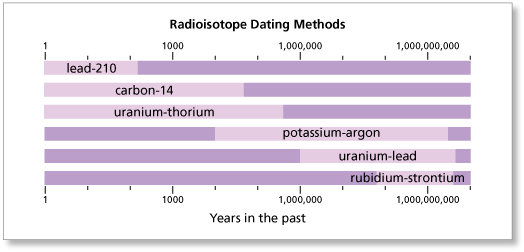
    d. Several methods of dating objects are shown in the diagram. Why do you think uranium-lead dating can be used to date older objects that carbon-14 dating cannot date?

     

    Comments (0)

    These comments are not screened before publication. Constructive debate about the information on this page is welcome, but personal attacks are not. Please do not post comments that are commercial in nature or that violate copyright. Comments that we regard as obscene, defamatory, or intended to incite violence will be removed. If you find a comment offensive, you may flag it.
    When posting a comment, you agree to our Terms of Use.

       _____     ___      _____     ______            
  / ___//   / _ \\   /  ___||  /_   _//     ___   
  \___ \\  | / \ || | // __     -| ||-     /   || 
  /    //  | \_/ || | \\_\ ||   _| ||_    | [] || 
 /____//    \___//   \____//   /_____//    \__ || 
`-----`     `---`     `---`    `-----`      -|_|| 
                                             `-`
    Showing 0 comments
    Subscribe by RSS
    There are no comments.
©Larson Texts, Inc. All Rights Reserved.